Capítulo 5 Análise de sobrevivência
Na análise de sobrevivência a variável dependente é o tempo até ocorrência de determinado evento. Compara-se a rapidez com que ocorreu determinado evento, ao contrário de comparar as percentagens de ocorrência deste evento ao final de determinado tempo.
É a técnica ideal para analisar respostas binárias (ter ou não ter um evento) em estudos temporais.
No momento da análise, podem haver indivíduos censurados, isto é, que não desenvolveram o evento até o fim do tempo de observação do estudo (independentemente do motivo).
5.1 Curva de sobrevivência de Kaplan-Meier
As curvas apresentam uma forma de “escada”. No eixo vertical está a porcentagem de sobrevivência, ou seja, a probabilidade de não ocorrer o evento.
5.2 Exemplo de uma Análise de Sobrevivência
Considere os dados presentes na planilha surv.xlsx.
Os dados representam a germinação de escleródios de S. rolfsii submetidos a tratamentos com óleo essencial de Cravo a 5000 ppm em diferentes tempos (30, 90 e 180 minutos).
A organização da planilha deve ser feita rigorosamente desta forma:
- 1ª coluna: nome dos tratamentos;
- 2ª coluna: número das repetições;
- 3ª coluna: número de indivíduos em cada repetição;
- 4ª coluna em diante: número de indivíduos que apresentaram o evento estudado com o nome das colunas representando o tempo;
- Última coluna: números de indivíduos censurados.
Caso esta organização seja seguida rigorosamente, podemos utilizar a função surv_data (download aqui) para preparar os dados para a análise de sobrevivência.
source("script/surv_data.R")
sobrev <- readxl::read_excel("data/surv.xlsx", skip = 2) %>% surv_data()Iniciamos então a análise com o pacote survival:
## Call: survfit(formula = Surv(time, status) ~ trat, data = sobrev)
##
## n events median 0.95LCL 0.95UCL
## trat=CR030 48 47 7.5 7 9
## trat=CR090 48 45 7.0 6 7
## trat=CR180 48 0 NA NA NA
## trat=TEST030 48 48 3.0 2 4
## trat=TEST090 48 48 3.0 2 4
## trat=TEST180 48 48 3.0 3 4
summary(an_sobrev, censored = TRUE)## Call: survfit(formula = Surv(time, status) ~ trat, data = sobrev)
##
## trat=CR030
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 3 48 2 0.9583 0.0288 0.903 1.000
## 4 46 6 0.8333 0.0538 0.734 0.946
## 5 40 3 0.7708 0.0607 0.661 0.899
## 7 37 13 0.5000 0.0722 0.377 0.663
## 8 24 7 0.3542 0.0690 0.242 0.519
## 9 17 6 0.2292 0.0607 0.136 0.385
## 10 11 1 0.2083 0.0586 0.120 0.362
## 12 10 9 0.0208 0.0206 0.003 0.145
##
## trat=CR090
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 3 48 3 0.9375 0.0349 0.8715 1.000
## 4 45 2 0.8958 0.0441 0.8135 0.987
## 5 43 8 0.7292 0.0641 0.6137 0.866
## 6 35 6 0.6042 0.0706 0.4805 0.760
## 7 29 14 0.3125 0.0669 0.2054 0.475
## 8 15 6 0.1875 0.0563 0.1041 0.338
## 9 9 5 0.0833 0.0399 0.0326 0.213
## 12 4 1 0.0625 0.0349 0.0209 0.187
##
## trat=CR180
## time n.risk n.event survival std.err lower 95% CI
## 12 48 0 1 0 1
## upper 95% CI
## 1
##
## trat=TEST030
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 2 48 23 0.5208 0.0721 0.3971 0.683
## 3 25 8 0.3542 0.0690 0.2417 0.519
## 4 17 12 0.1042 0.0441 0.0454 0.239
## 5 5 4 0.0208 0.0206 0.0030 0.145
## 6 1 1 0.0000 NaN NA NA
##
## trat=TEST090
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 2 48 19 0.6042 0.0706 0.4805 0.760
## 3 29 9 0.4167 0.0712 0.2981 0.582
## 4 20 11 0.1875 0.0563 0.1041 0.338
## 5 9 7 0.0417 0.0288 0.0107 0.162
## 6 2 2 0.0000 NaN NA NA
##
## trat=TEST180
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 2 48 11 0.7708 0.0607 0.6606 0.899
## 3 37 18 0.3958 0.0706 0.2791 0.561
## 4 19 8 0.2292 0.0607 0.1364 0.385
## 5 11 8 0.0625 0.0349 0.0209 0.187
## 6 3 3 0.0000 NaN NA NAComparação pareada (pairwise) entre duas curvas de sobrevivência utilizando o teste G-rho (logrank test).
No exemplo abaixo, testou-se a diferença entre os tratamentos TETS090 e CR090.
sobrev %>%
filter(trat == "TEST090" | trat == "CR090") %>%
survdiff(Surv(time, status) ~ trat, data = .)## Call:
## survdiff(formula = Surv(time, status) ~ trat, data = .)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## trat=CR090 48 45 72 10.1 69.9
## trat=TEST090 48 48 21 34.5 69.9
##
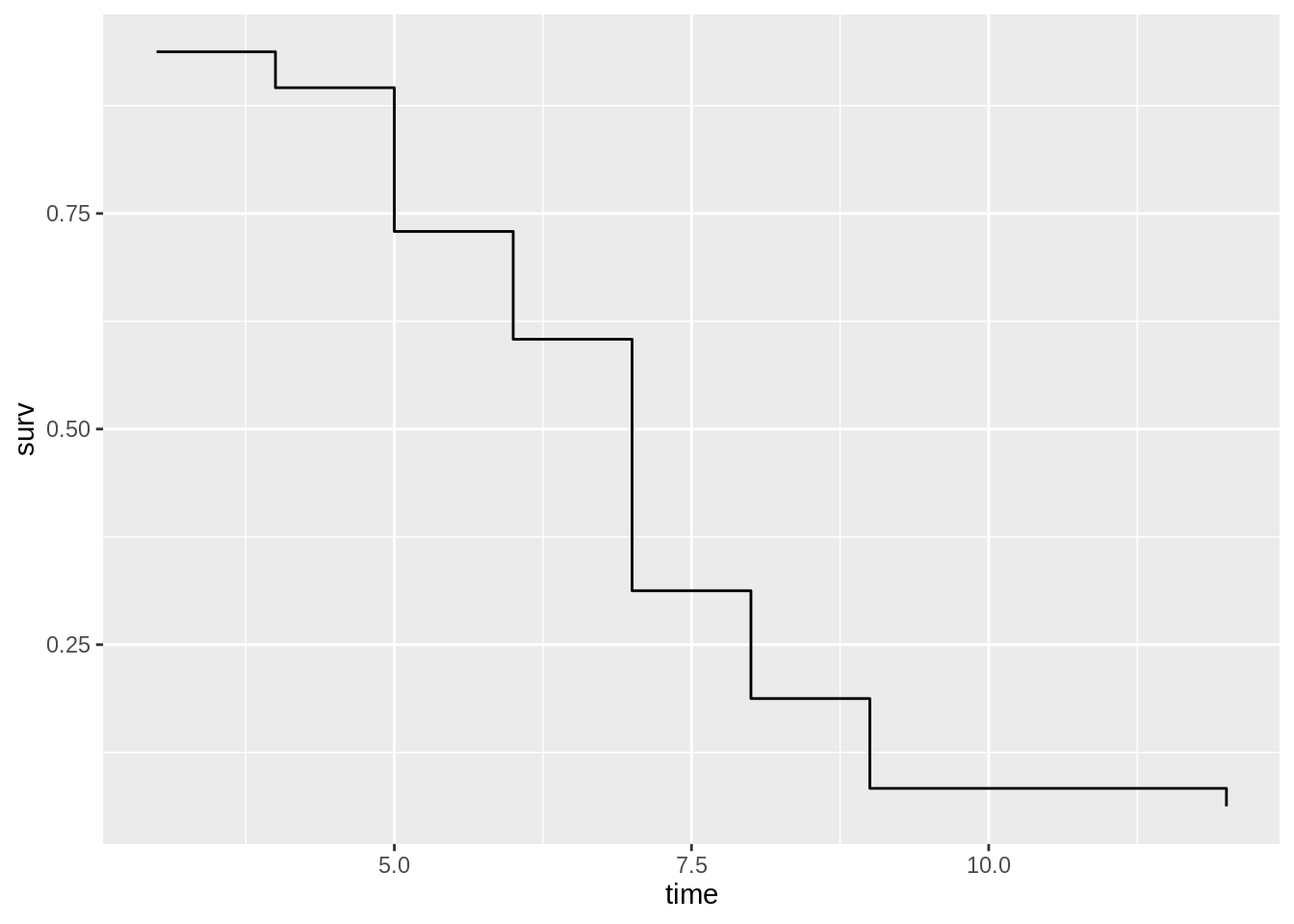
## Chisq= 69.9 on 1 degrees of freedom, p= <2e-16E as curvas de sobrevivência podem ser plotadas com o pacote ggplot2, utilizando a geometria geom_step.
g_surv <- data.frame(
trat = summary(an_sobrev, c = T)$strata,
time = summary(an_sobrev, c = T)$time,
surv = summary(an_sobrev, c = T)$surv
)
library(ggplot2)
g_surv %>%
filter(trat == "trat=CR090") %>%
ggplot(aes(x = time, y = surv)) +
geom_step()